It was once thought in the past that numbers arranged in a particular pattern are mysterious and magical. But now-a-days it is clear that they are just ways of arranging numbers using certain rules.
A Chinese myth says that while walking along the Yellow River Emperor Yu found a tortoise with a pattern on its shell. He called this unique diagram Loh–Shu. It was a 3 × 3 magic square with symbols rather than numbers.

The Loh–Shu Magic Square
From the China, Magic squares were introduced to India. The first magic square of order four was discovered by Swancy in 2000.
To day applications of magic squares are found very rare.
Q : What do you mean by magic squares?
Ans : Magic squares are the squares in which the sum of the numbers in each row, column and along each diagonal is the same. The basic square of order n can be defined as an arrangement of numbers from
1 to n2 in an n × n matrix such that the magic sum or the number that each row, column and diagonal add upto be same. There are several methods of generating magic squares.
Q : What is the method of construction of 3 x 3 Magic Square?
Ans : (a) A 3 × 3 Magic Square can be constructed by any set of nine numbers having equal difference between them.
(b) Once 9 is filled in the centre there are eight boxes to be filled. Four of them will be below 9 and four of them above it.
For Example;
(i) 5, 6, 7, 8 and 10, 11, 12, 13 with a difference of 1 between each number.
(ii) 1, 3, 5, 7 and 11, 13, 15, 17 with a difference of 2 between them.
(iii) -11, -6, -1, 4 and 14, 19, 24, 29 with a difference of 5.
Now decide any set of numbers you want to take,
(c) Draw a square having three rows with three squares.
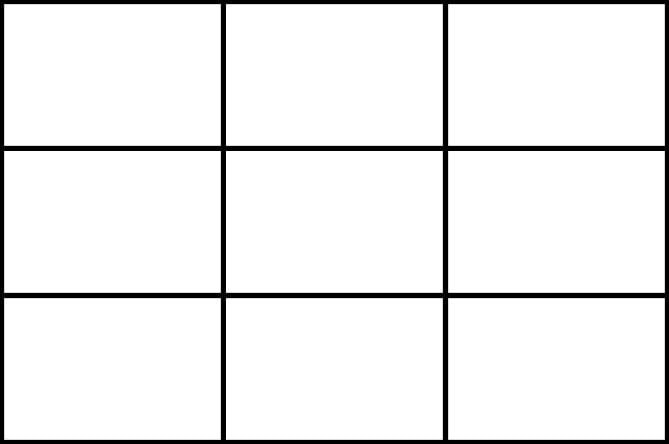
(d) Draw four projected squares on the middle square of the each side as shown below.
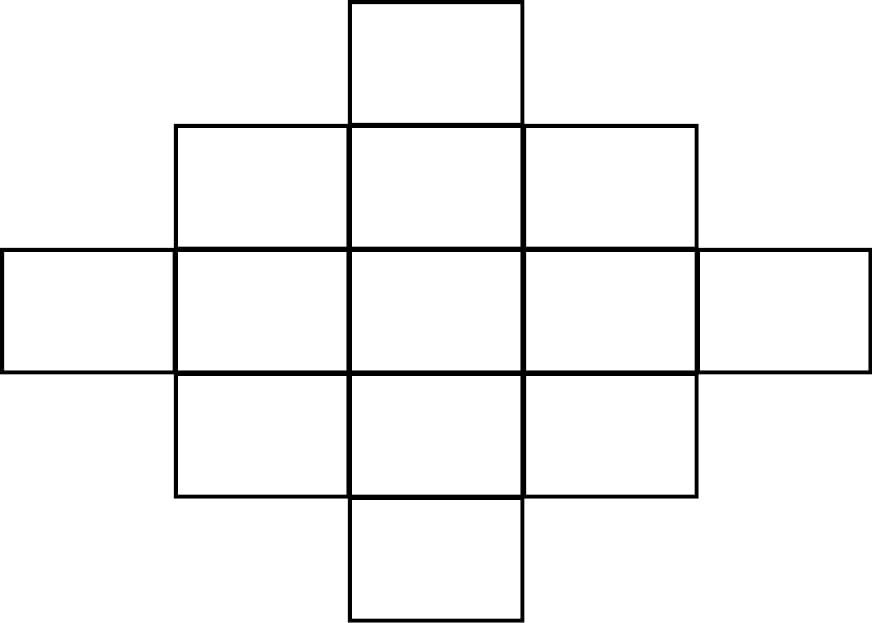
(e) Now three diagonals with three squares in each are formed alternatively.
(f) Enter the numbers in the diagonal squares as shown below.

(g) The number from each of the projected square is transferred to the empty square
on the opposite side as shown below.
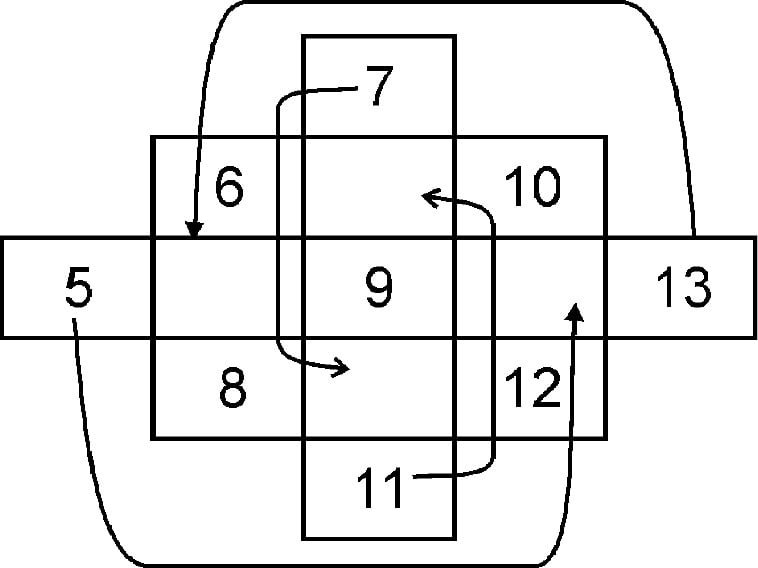
(h) After transferring the numbers 3 × 3 magic square is formed in which the sum of the numbers in each row, each column and along each diagonal is the same as 27 i.e
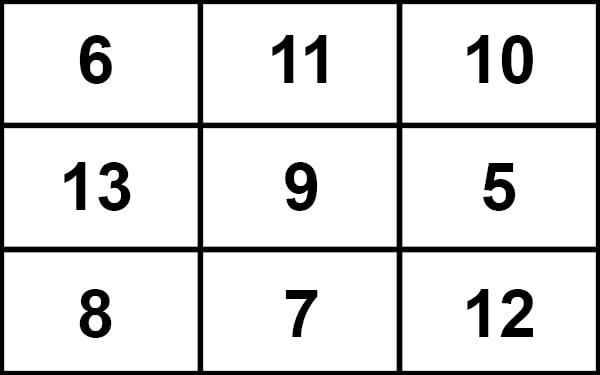
(i) In 3 × 3 magic square the magic sum is
three times the middle number.
Other examples of 3 × 3 magic square are;
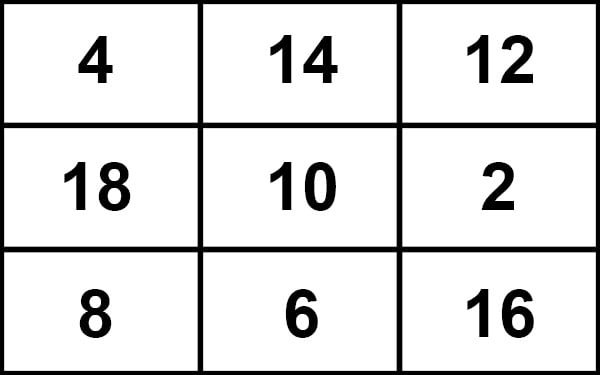
Fig 1
The magic sum of above fig 1 is 30 which
is middle number × 3. i.e. 10 × 3 = 30
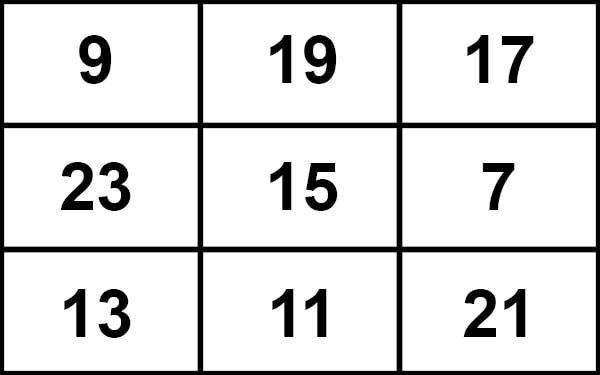
Fig 2
The magic sum of above fig 2 is 45 which
is 15 × 3.
Now you try with other numbers.
Q : What is the method of construction of 4 × 4 magic square?
Ans : A 4 × 4 magic square can be constructed by any set of sixteen numbers with an equal difference between them.
(a) Draw a square having four rows with four
squares in each. As shown below;
(b) Select a set of sixteen consecutive numbers
with a common difference.
For Example;
(i) 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
and 16.
(ii) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27,
29 and 31.
(iii) 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26,
28, 30 and 32.
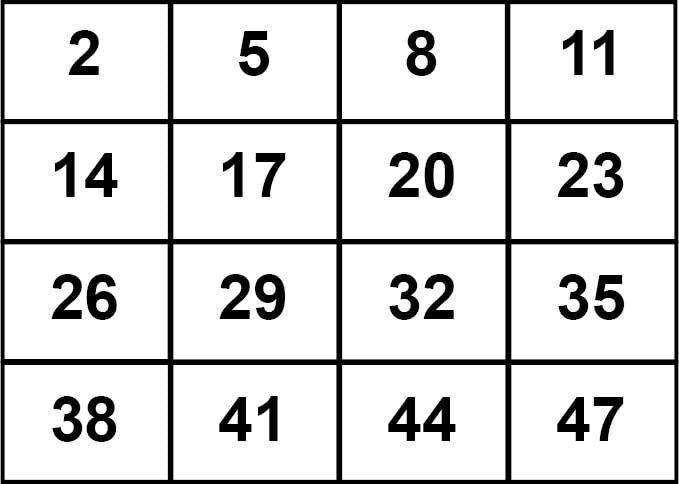
(iv) 2, 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35, 38,
41, 44 and 47.
The magic sum in first case is 34.
The magic sum in second case is 64.
The magic sum in third case is 68.
The magic sum in fourth case is 98.
(c) Now write them in order from the beginning of the first small square in the
first row to the last small square in the last row as shown below.
(d) Now write the diagonals in reverse order as shown below.
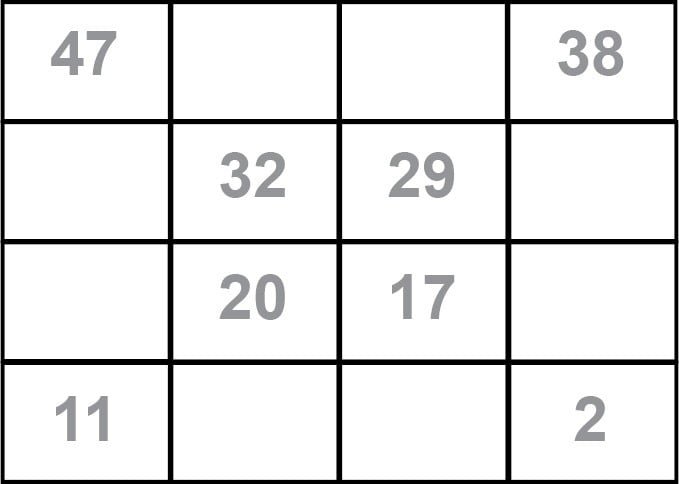
(e) Now fill the numbers with above diagonals.
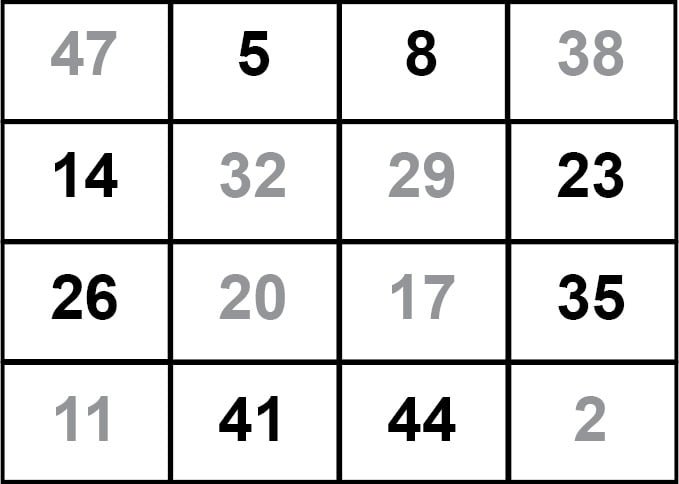
(f) Thus a 4 × 4 magic square is formed in which the sum of numbers in each row, in
each column, along each diagonal, the four middle numbers each of the four small 2 × 2 squares at the corners is the same as 98.
(g) Some other examples of 4 × 4 magic square are as following.
Example I
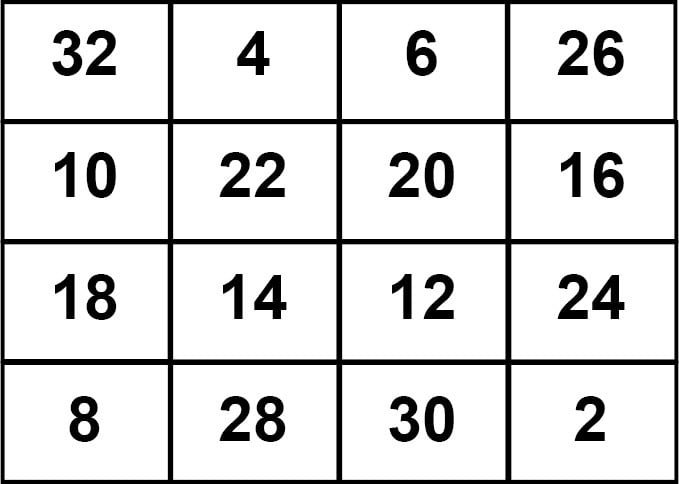
The magic sum is 68
Example II

The magic sum is 34
(h) Now you try with other numbers.
Semi Magic Squares
Let us find some easy way to prepare simple magic squares of order 4 to n and their magic sum without calculating and preparing the magic square. The conditions which are to be followed are following :
1. The order of magic square starts from 4 onward.
2. Simple consecutive numbers start from one as 1,2, 3, 4………….. are taken to fill the grid in order from the beginning of the first box in the first row to the last box in the last row.
3. The magic sum in each square will be the numbers that each diagonal and the middle lines from each side add up to be same.
4. In case of even order the sum will be average sum of the two middle lines.
5. The magic sum of the magic square of order n will be by the formula n (n2 + 1).
For Example;
(a) Let us prepare 5 × 5 magic square.
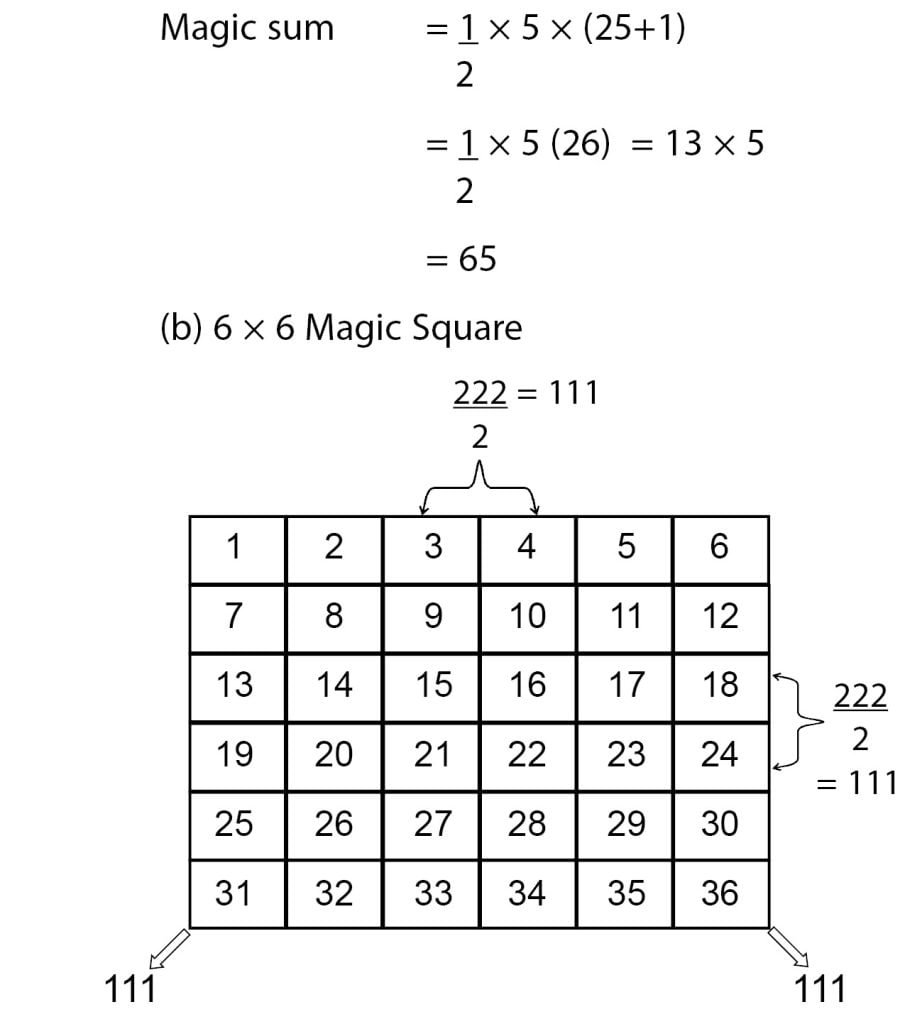

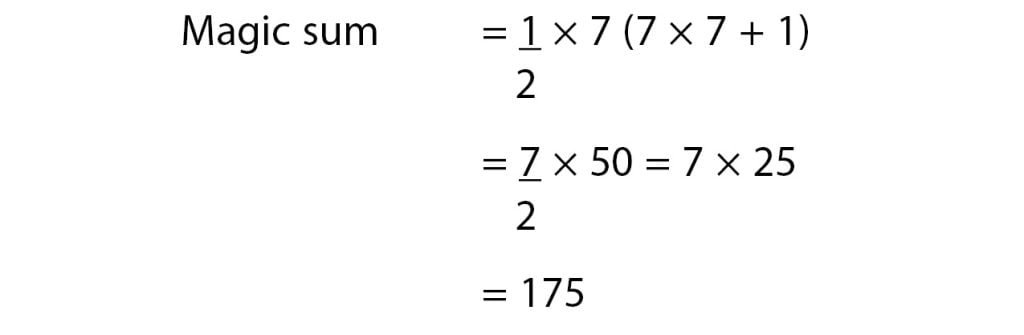
Similarly, we can prepare n number of Semi Magic Squares.
Let us do some amendment with 6 × 6 square.
First of all draw a 6 × 6 square by writing all the numbers in order from top left of a square to the bottom right.
Now high light the two rectangular blocks as follow.
Invert the IInd rectangular block

Now rewrite diagonals in reverse order as follow.

1. You will see all the rows will sum up to be same as 111.
2. All the numbers of both diagonals in average will sum up to be same as 111.
Magic Squares
The Stair case Method or Siam Method for odd order Magic Squares
Let us learn how to make a complete 3 × 3, 5 × 5,
7 × 7 and 17 × 17 magic squares.
1. All the above squares can be made by the Siam method.
2. Here the order (n) of the magic square is odd number, which tells that there will be a middle column and a middle square in the top row.
3. Take simple consecutive natural numbers starting from 1 onwards.
4. The basic rule for doing this is that one counts diagonally upwards to the right this is called stair case method.
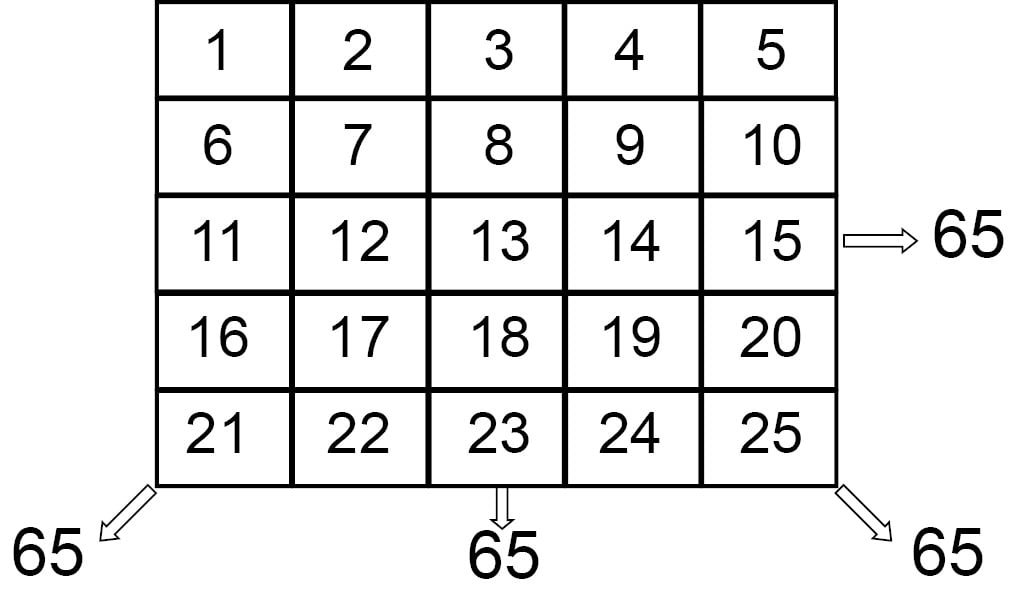
For example : We prepare here a 5 × 5 magic square with the following steps for you.
1. The order (n) of the magic square is 5.
2. The magic sum will be
M.S. = 1/2 n (n² + 1)
= 1/2 × 5 (25 +1)
= 1/2 × 5 (26)
= 5 × 13 = 65
This means that every row, column and diagonal add up to be same as 65.
3. Begin with 1 putting in the middle square of the top row.
4. Now it is impossible to move diagonally upwards from this position because we are already at the top of the square.
For this, if you are at the top come to edge pretend that the top edge is pasted to the bottom edge and come to the bottom. Therefore, after 1 we place 2 in the bottom row in the square right to the middle column.
5. Now move diagonally upward to the right which is same as moving right one column and up one row fill numbers 3.
6. After filling 3 in the right most column come to the left most column moving one row up put the No 4.
7. After filling 4 move diagonally upward to the right and fill number 5.
8. For number 6, the square we would like to put 6 is already having the number 1. When this happens just drop down one square from the square one is at present. So 6 will be placed directly below 5.
9. Again move diagonally upward to the right and fill the number 7 and 8.
10. Now number 8 is in the top most row so we follow the first rule of pretending to consider the bottom most row the top most row and fill the number 9 in the next right column.
11. To fill 10 we have to move left most column in one row above as 9 is the leftmost row.
12. For number 11 drop down to the square below the number 11.
13. Again move diagonally upward to the right and fill the numbers 12, 13, 14, 15.
14. For 16 drop down to the square below the number 15.
15. Because 16 is in the rightmost column now move to the leftmost square with one row above and fill the number 17.
16. Now 17 is at the topmost row, now fill 18 in the bottommost row with one column to the right.
17. Again move diagonally upward to the right and fill the numbers 19 and 20.
18. Drop down below 20 and fill 21.
19. Again move diagonally upward to the right to fill 22.
20. Because 22 is in the right most column so fill 23 in the leftmost column with one row above.
21. Again move diagonally upward to the right and fill the number 24.
22. Because 24 is in the topmost row so for 25, come to the bottom most row with one column to the right.
Hence a magic square 5 × 5 of order five is formed with magic sum 65.

In the figure above each row column and diagonal add up to be same as 65 which is the magic sum.
The same method can be used to make a 3 × 3 magic square, 7 × 7 magic square and 17 × 17 magic square.
Example of 3 × 3 magic square
Magic sum = ½ × 3 (3²+1)
= ½ 3 (10) = 15

Example of 7 × 7 magic square
Magic sum = ½ × 7 (7²+1)
= ½ × 7 (49+1)
= ½ × 7 X 50
= 7 × 25 = 175
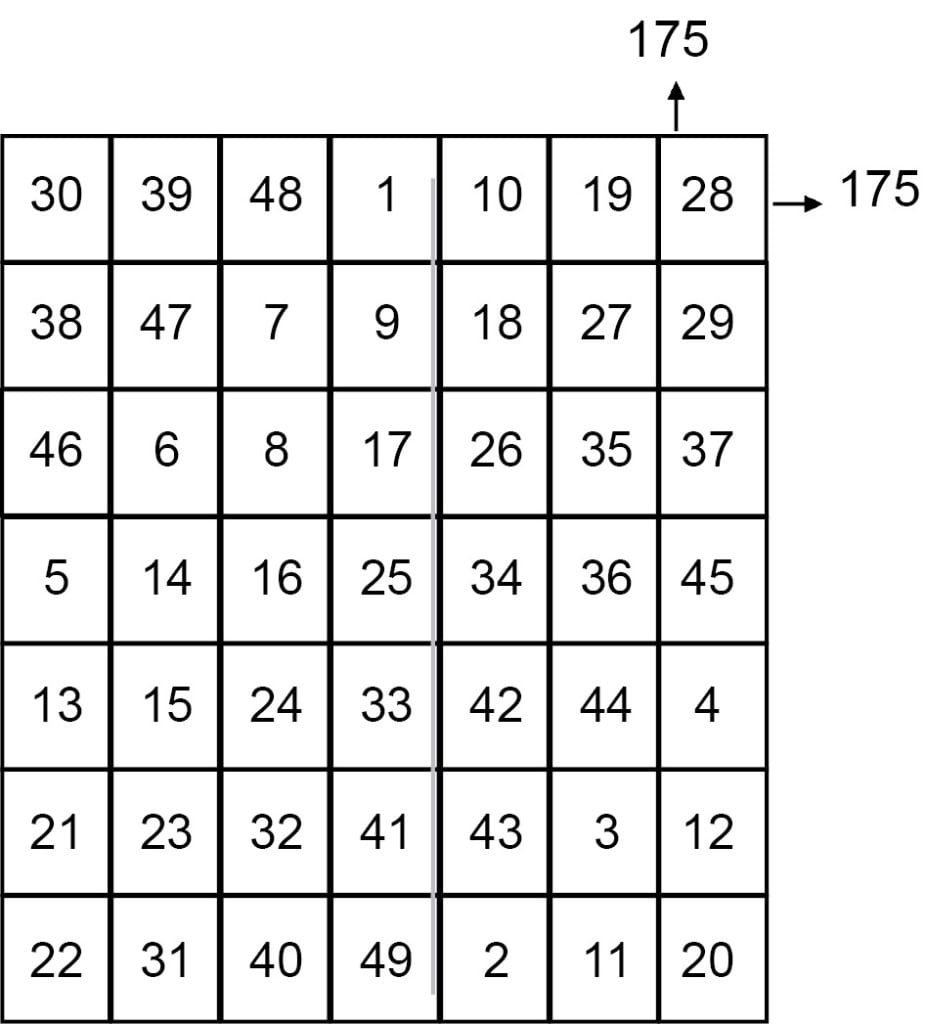
Magic Square with more introduction
An algorithm which works for odd order will not work for even order squares.
While making odd order square till now I have used only staircase method, now I will prepare the same with Pyramid Method.
Let us prepare a 3 × 3 magic square by the Pyramid Method with following steps.
1. Draw a pyramid on each side of the magic square. That means draw symmetrically one square extra on the each middle column and row on the outer side. This is because to make a pyramid the magic square should have two less squares on its base than the number of squares on the side of the magic square. This shows a square standing on a vertex.
2. Now place the numbers using consecutive numbers starting from 1 and ending with the square of the order i.e. n².
3. Relocate the number which is not in the nxn square which appears in the pyramid to the opposite hole inside the square as shown below.
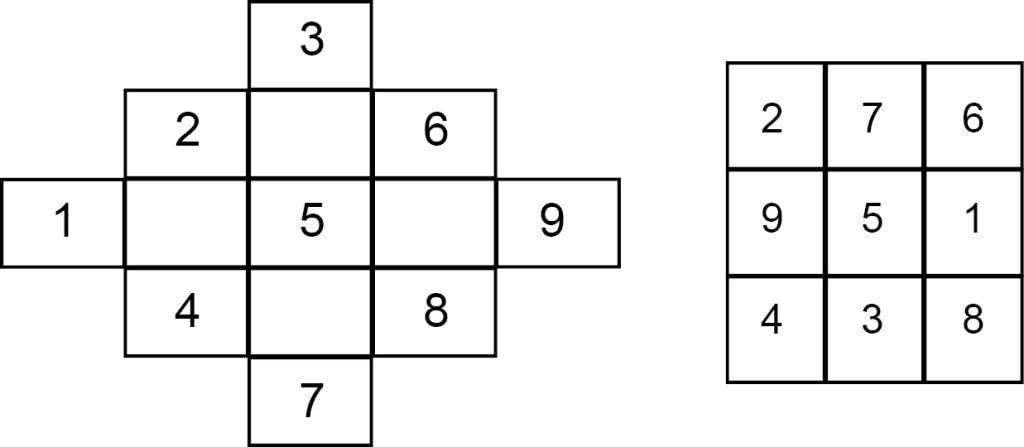
The same pyramid method can be used for any odd order magic square.
Let us take the example of 5 × 5 square.
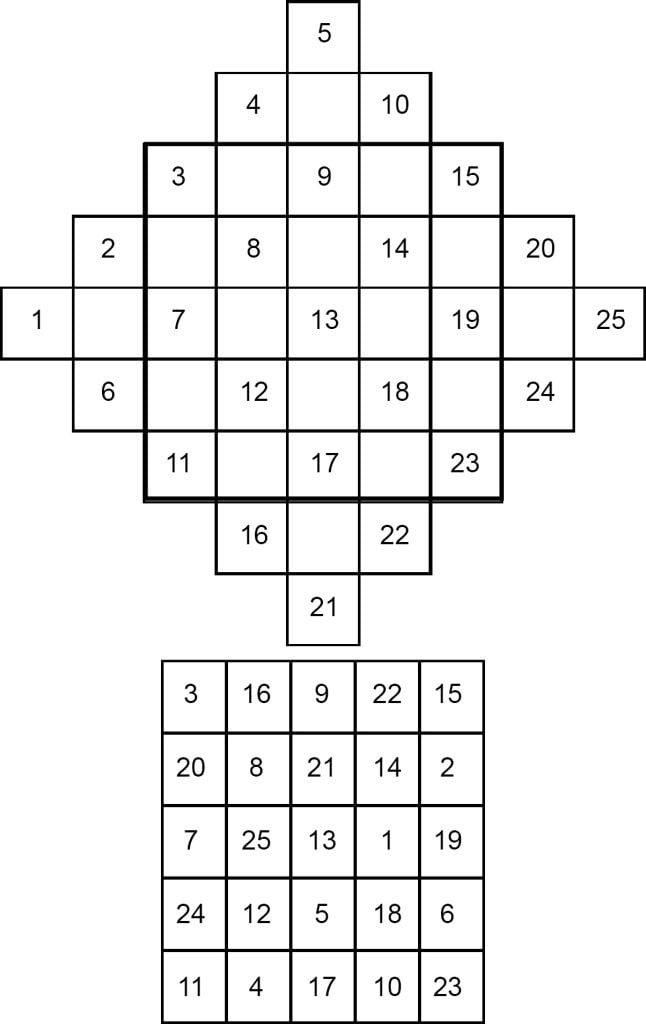
Properties of Magic Squares
1. Magic square where the first number is 1 is called the Traditional Magic Square.
2. When the lowest number is zero in a Magic Square we call it as Zero Origin Square.
3. It is easier to prepare Zero Origin Magic Square than Tradition Magic Square.
4. To convert a Magic Square starting at zero to a Traditional Magic Square add one to each cell in the square.
5. There are several methods of generating the magic squares.
6. A magic square will remain magic if any number is added to every number of a magic square.
7. A magic square will remain magic if two rows, or columns, equidistant from the centre are interchanged.
8. A magic square will remain magic if any number multiplies every number of a magic square.
9. An odd order magic square will remain magic if the partial quadrants and the row is interchanged.
10. An even order magic square (n × n where n is even) will remain magic if the quadrants are interchanged.
Paired Exchange Method for Even Order Magic Square
This method can be applied to prepare any type of even number Magic Square. We will learn how to prepare even order magic square with the “Paired Exchanged Method.”
Remember there are no 2 × 2 Magic Squares.
Follow the steps of ‘Paired Exchanged Method’:—
1. Consider the first and last column of a n × n magic square where n is even.
2. Place the integers in order across the rows putting the first number in the first box of the first row of the square and last in the last box of the last row of the square.
3. The difference between the first and the last number in any row will be n-1.
4. Since there are n rows in the square, there will be a total difference of n (n-1) between the first and last column of the square.
5. To balance the total for the first and last columns we must exchange pairs of numbers between the first and last columns and each exchanged pair must be from the same row, so as not to change the sum total of the row.
6. When a pair is exchanged in a row the difference between the columns changes by 2 (n-1).
Thus, if
t = the number of times pairs must be exchanged.
Then
t [2(n-1)] = n (n-1)
2t (n-1) = n (n-1)
2t = n
t = n/2
7. Same reason can be made for the second and the next to last columns by substituting (n-3) for (n-1). The resulting t stays the same.
8. All columns paired from the centre line of the square can be made to be equal to the magic sum.
9. Similarly all rows can be made to equal the magic sum.
Let us discuss a few examples
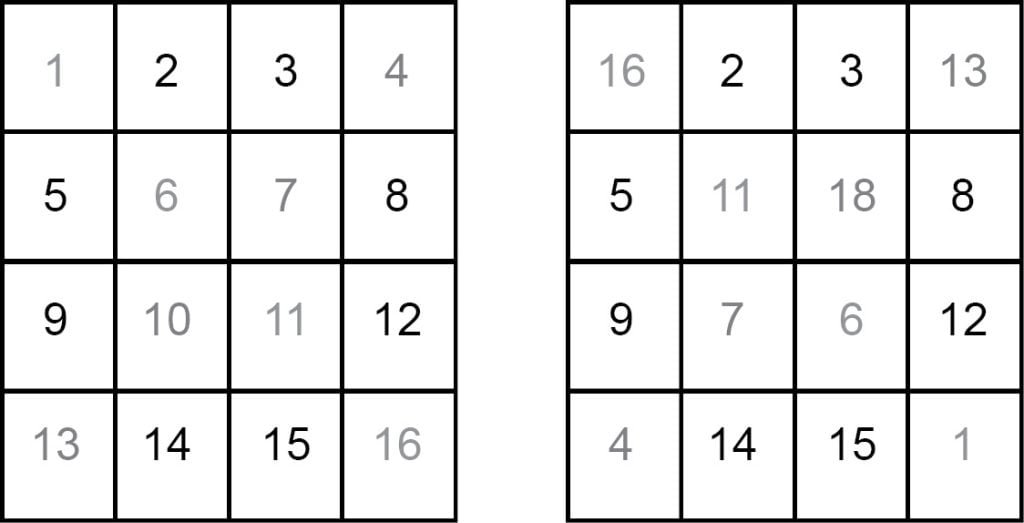
Take 4 × 4 magic square
(a) t is equal to 2 by putting values in the formula
t [2(4-1)] = 4 (4-1)
2t (3) = 4 (3)
2t = 4 × 3 = 4
3
t = 2
(b) Now exchange the numbers with their opposite numbers equidistant from the centre along the diagonals.
(c) We have exchanged two pairs in each row and column of the square and the result is a magic square. Or you just reverse the order of the diagonals.
Let us take 6 × 6 magic square
- Here t = 3
- Now exchange all the pairs on the diagonal which is reversing the order of diagonal.
- In addition to this exchange one more pair from each pair of rows and columns should be exchanged to get the magic sum.
Fig I
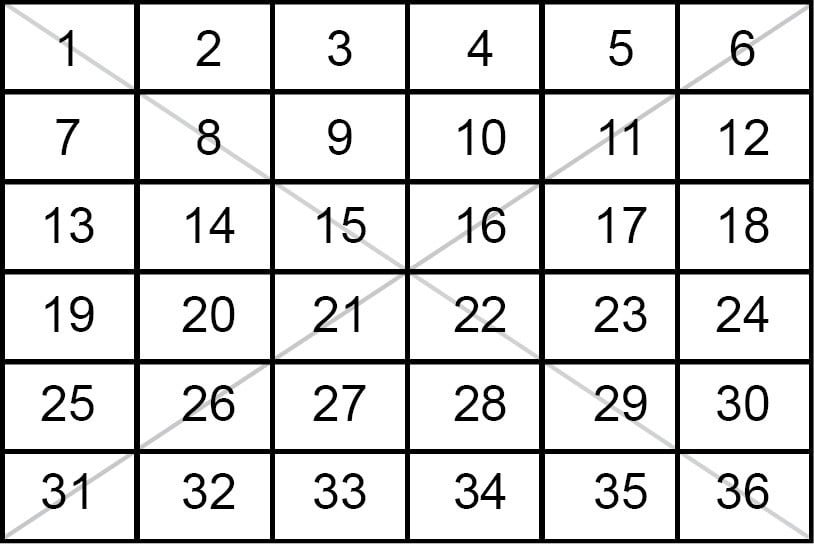
Fig II
Reverse the order of diagonals

Fig III
Equalizing the columns by exchanging the pairs
in the columns.

Fig IV
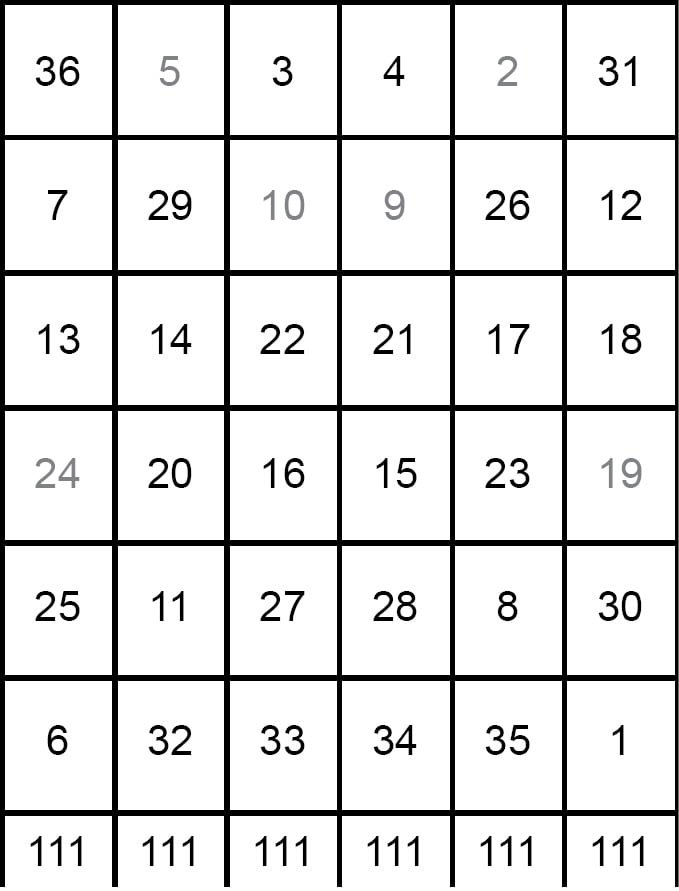
Fig V
Equalizing the rows by exchanging the pairs in the rows.
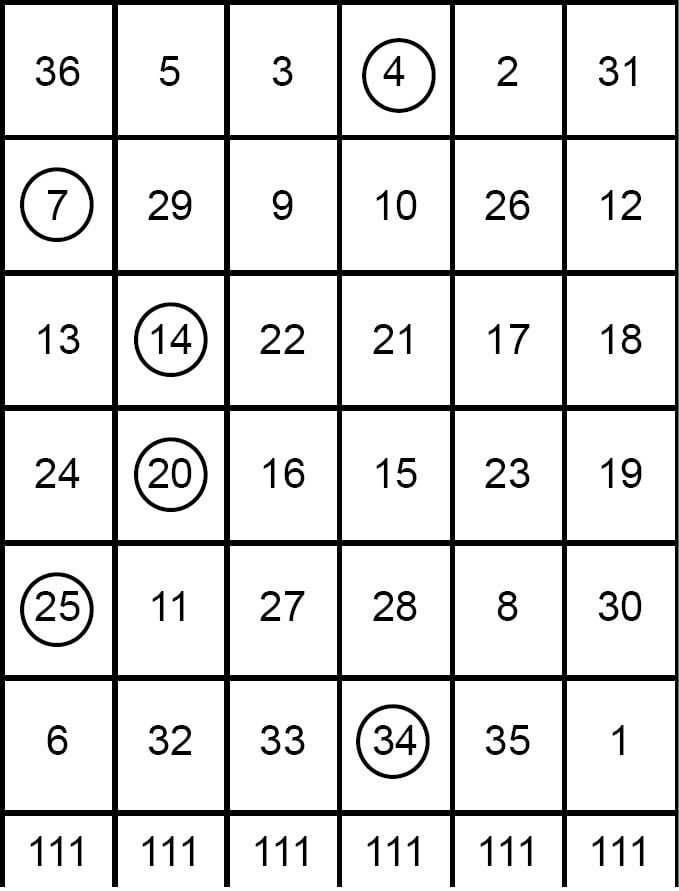
Fig VI

Some other Methods for Making Even order Magic Squares of order (4n + 2)
1. Even order magic squares of type (4n + 2) would have order 6, 10, 14, …..
2. Remember till now we have learned the Siam method or staircase method.
3. Let us discuss a 6×6 magic square with this method.
4. First of all we partition the 6 × 6 square into four 3×3 blocks
Fig

5. In the upper left hand block we enter the numbers 1 to 9 by staircase method, as shown in fig (a).
6. Then we fill the numbers from 10 to 18 using the staircase method in the lower right hand block, as shown in fig (b).
7. Now we enter the numbers from 19 to 27 by the staircase method in the upper right hand block as shown in fig (c).
8. At the end, enter the numbers 28 to 36 in the lower left hand block, getting the square at right in the fig (d).
Fig (a)
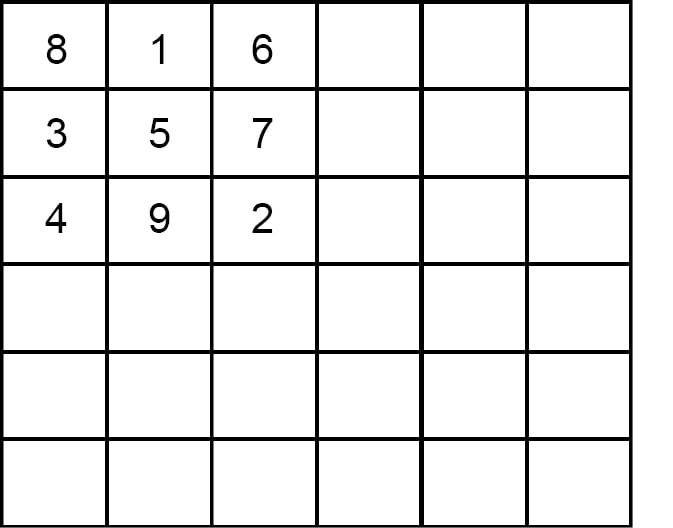
Fig (b)
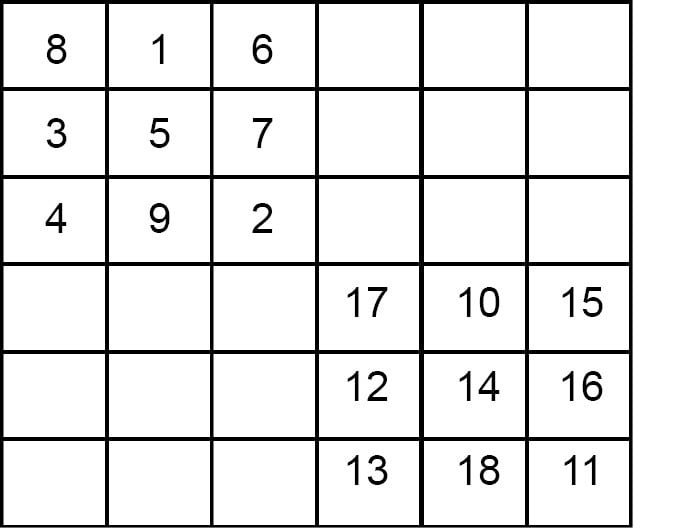
Fig (c)
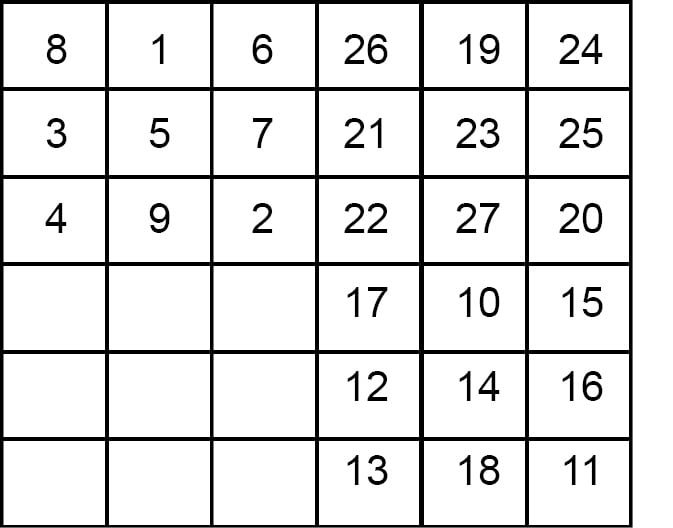
Fig (d)
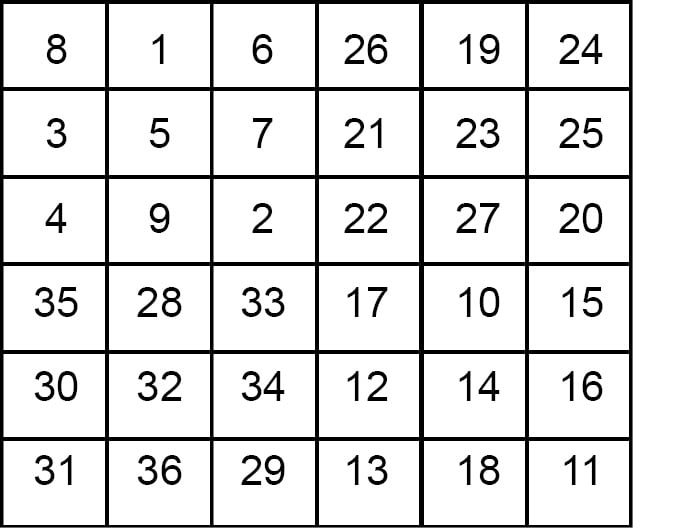
9. Remember staircase method should be used twice. One while filling each block and second while choosing the block to be filled next.
10. In the fig (d) all the columns sum upto be 111.
11. The rows do not favour the sum 111.
12. The first three rows sum to 84 and the last three sum to 138.
13. If we change an element in row one it must be exchanged with another element in the same column to maintain the sum of 111.
14. To get a sum of 111 in row one, we must increase the value of an element in that row by 27, since
111 – 84 = 27.
15. There are three choices. Any one of the first three entries in row one can be exchanged with their corresponding entry in row four.
16. Similarly, we can exchange the numbers in all the rows within the same columns to sum up to be the same sum as 111.
17. Sometimes in such cases the diagonals do not sum to 111. Such problems can be sorted out by exchanging the numbers lying on the two diagonals but in the same column. As 5 can be exchanged with 32 which are diagonal numbers and so on.
18. The desired 6×6 magic square is as follows :

19. Similarly we can prepared n number of even number squares.
20. Here is an example of 10 × 10 magic square. Prepare this square similarly as following the above steps. Used in 6 × 6 magic square partitioning the square in four blocks of 5 × 5 squares.
Fig I

10 × 10
Magic Square
Note : In general if we want to create a magic square of order n = 4K+2 then we begin by partitioning the square into four (2K+1) x (2K+1) squares.
Let us study the pattern for a general (4n+2) x (4n+2) Magic Square
In case of 6×6 Magic Square 6 = 4 × 1 + 2
.·. n = 1
This means we are to change elements in column one except for the two diagonal elements.
In case of 10 x 10 Magic Square
10 = 4 × 2 + 2
.·. n = 2
This means we are to change elements in the first two columns, except for the diagonal elements and the last column.
Similarly, in case of 14 x 14 Magic Square
14 = 4 x 3 + 2
.·. n = 3
If we change the first three columns except for the diagonal elements, and the last two rows we might get a 14 x 14 Magic Square.
Now the rule is in (4n + 2) x (4n + 2) square, we would change the first n columns except for the diagonal elements and the last n – 1 columns.
Applying this rule to the 14 x 14 square we get the following square which is a magic.
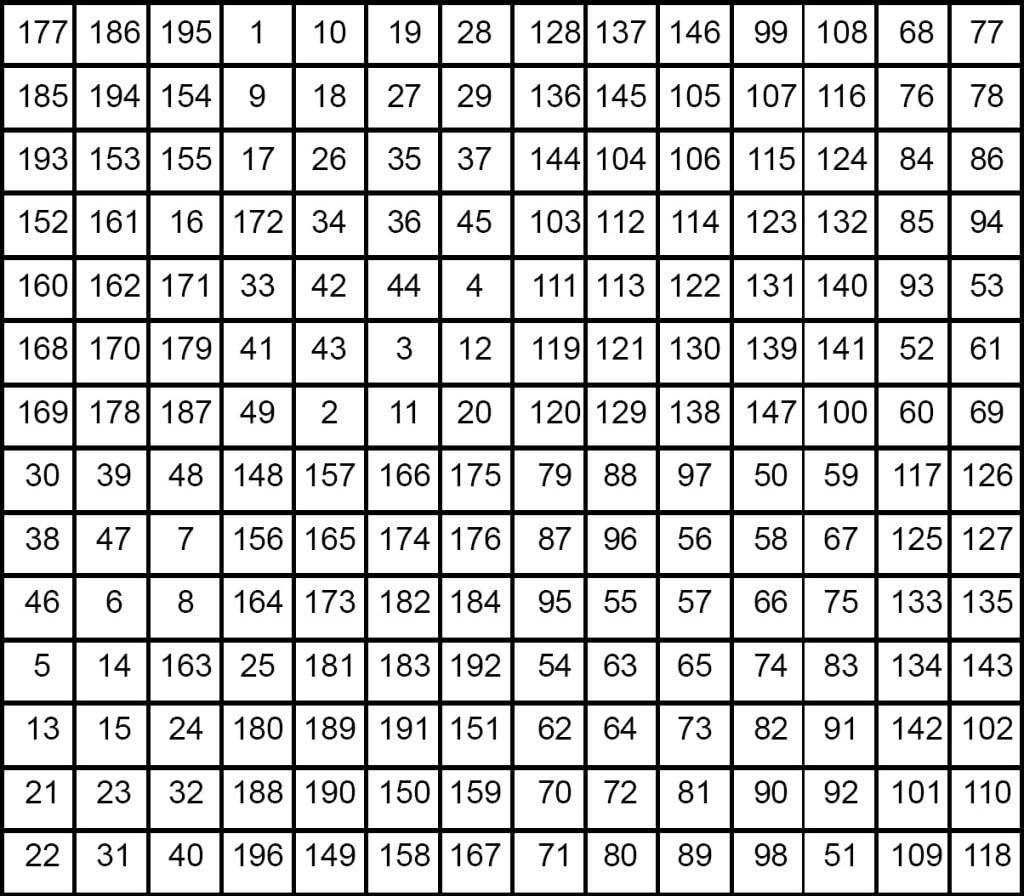
Some More
We have already learnt Stair Case Method for magic squares. We used stair case method is 3 × 3 and 5 × 5 but it did not work on 9 x 9 magic square.
But with a few differences it will work on 9 × 9 magic square also.
1. We are to fill this square from 1 to 81.
2. First of all divide the 9 × 9 square into nine 3 × 3 blocks as follow :—

1. Fill each block with the stair case method.
2. You should also know which block should be at first, at second and so. Remember select the block to be filled next in a stair case way.
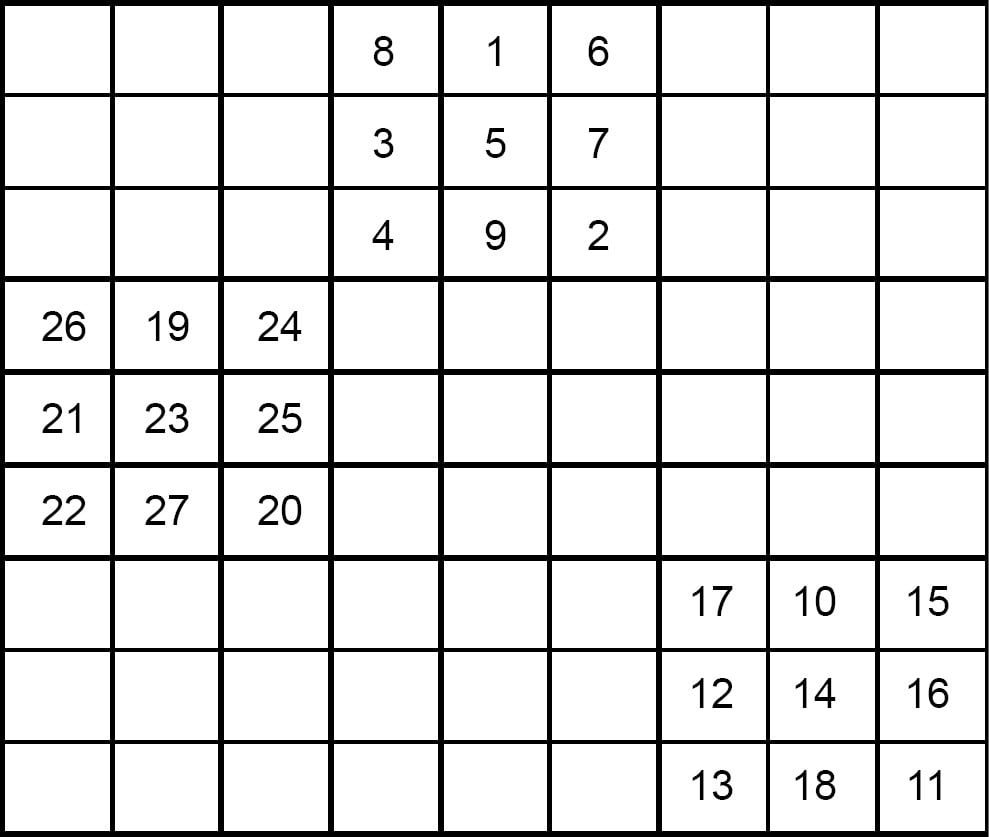
Rest of the numbers you fill yourself and check if
9 × 9 magic square is formed or not.
Cross Method When the Square is Multiple of Four
When n = 4 m
Let us take the example of when order of square = 8
Where n = 4 × 2
1. Write all the numbers in order from the top left of a square to the bottom right.
2. Four 4 × 4 block are formed.
3. Draw diagonals in each 4 × 4 block. You may use different colours for that.
4. Now swap the numbers along the diagonals of the cross as follow :
(a) Left to right cornered diagonal numbers of block I should be reversed and placed at the place of left to right diagonal of block IV.
(b) Similarly, left to right cornered diagonal numbers of block IV should be reversed and placed at the place of left to right diagonal of block I.
(c) Now right to left cornered diagonal numbers of block II should be reversed and placed at the place of right to left diagonal of block III.
(d) Similarly, right to left corned diagonal elements of block III should be reversed and placed at the place of right to left cornered diagonal of block II.
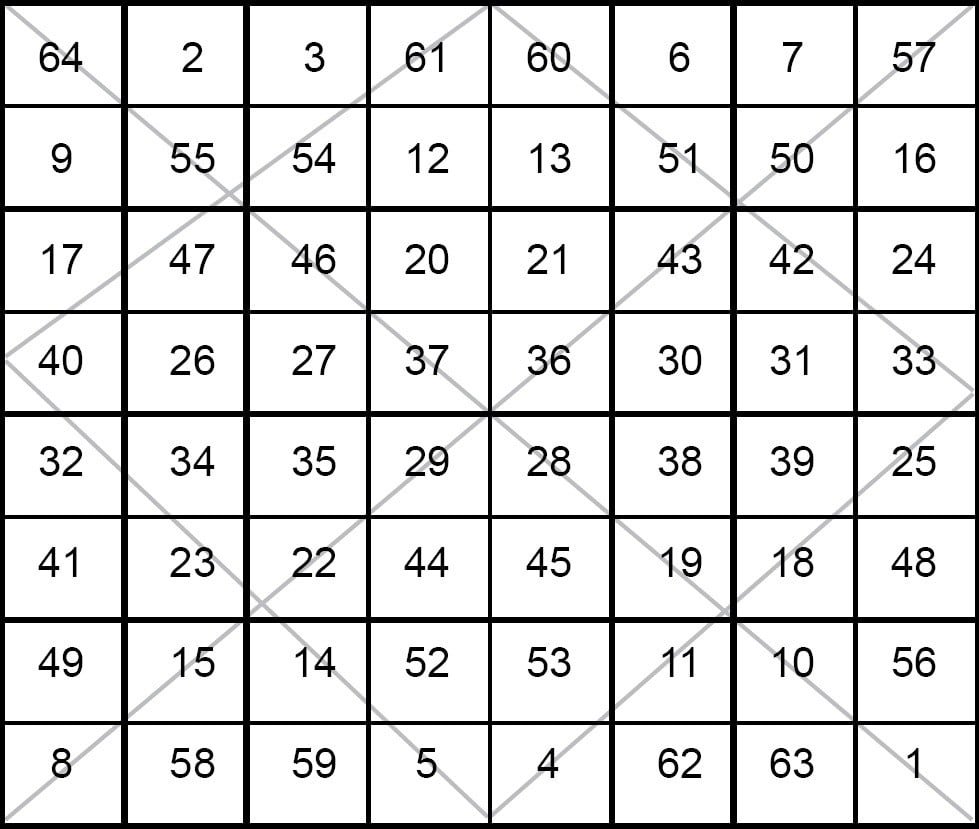
I II
260 III 260 IV 260

