The world of Math is fullof wonders. Once you start playing with these numbers you will create interest in math. In this section we will deal with simple problems which will activate your reasoning power.
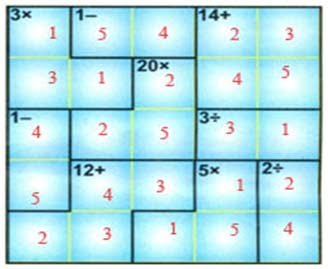
Q.No.1
Rules : (a) Fill number 1 to 5 without repeating the number in each row and column.
(b) The result of each block is given on the top left corner of the block where as the operation should be carried is given on the top right corner of the block.
Q.No.2
(a) Fill the boxes from 0 to 9.
(b) The sum of each column, row and diagonal lines are given.

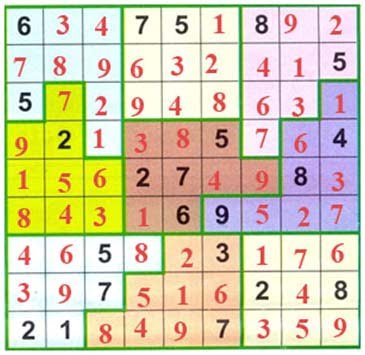
Q.No.3
Fill the numbers from 1 to 9, in such a way that
every row, column and grid made by thick lines
should not repeat any number from 1 to 9.
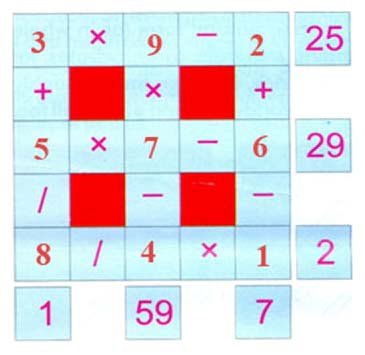
Q.No.4
Fill numbers from 1 to 9. The numbers should be used only once.
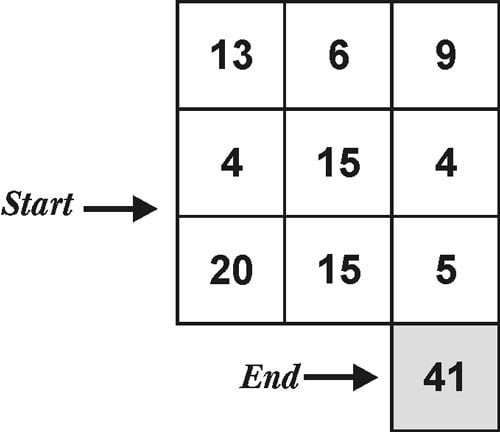
Q.No.5
Start from the number at the “Start Position”, moving either horizontally or vertically adding all the numberson the way and find the number at the “End Position”.
Q.No.6
How many triangles are there in the following geometric patterns?
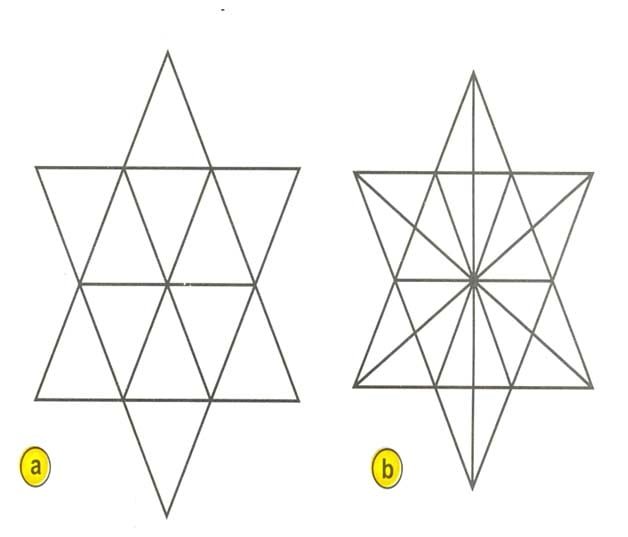
Q.No.7
Place numbers at the wall such that each number is the sum of two numbers just below it.

Q.No.8
Place the numbers 1 to 9 in such a way that the sum of each line of 3 numbers is 18 when the numbers are counted in a straight line.

Q.No.9
Fill the numbers 1 to 9 in such a way that each row and column should not repeat the number. The results of the operations of each row and column are given in the last box of row and column respectively.

Q.No.10
All the squares are equal in area. Divide the squares in three equal parts in continuity. Each part includes one electrical pole.

Q.No.11
Fill the grid with the number 1 to 5. Each column and each row must contain different numbers.

Q.No.12
There are twenty numbers from 1 to 20. Arrange them into six unequal groups such that each group when add equals to 35.
1 2 3 4 5 6
7 8
9 10 11 12
13 14 15 16 17 18 19 20
Q.No.13
Visit all the twenty dots given in the circle such that each dot should be visited only once.Travel only along the white lines. Finish the journey at the dot from where you have started.You can start from any point.

Q.No.14
(a) Starting from any number find the highest total you can make by adding the number on the route you move.
(b) You are neither allowed to jump any number nor to go back over a path twice.
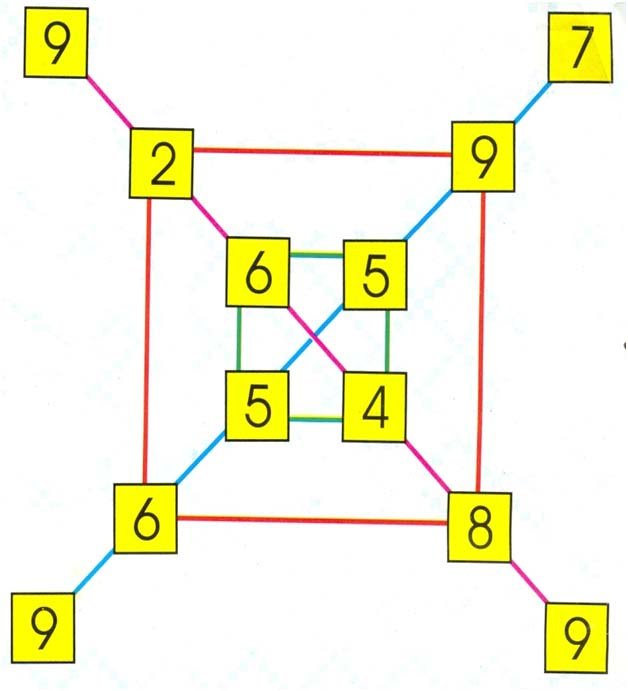
Q.No.15
Using each number once fill the following rows and columns with the numbers 1 to 9. The operations of numbers in each row and column give the result to the right and along the bottom respectively.
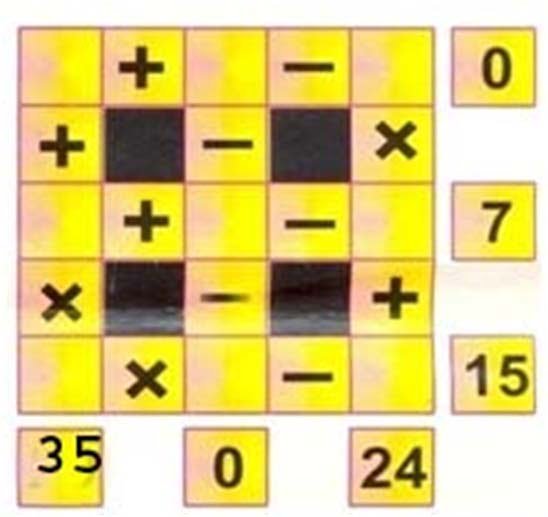
Q.No.16
Fill the boxes from 0 to 9 without repeating any number such that sum of four outside numbers should equal to the middle number. The product of top two numbers is equal to the middle number and sum of three numbers on a line is equal to the other three numbers on the other line.

Q.No.17
Fill the numbers 1 to 9 in the boxes so that each side of the triangle adds up to 20.
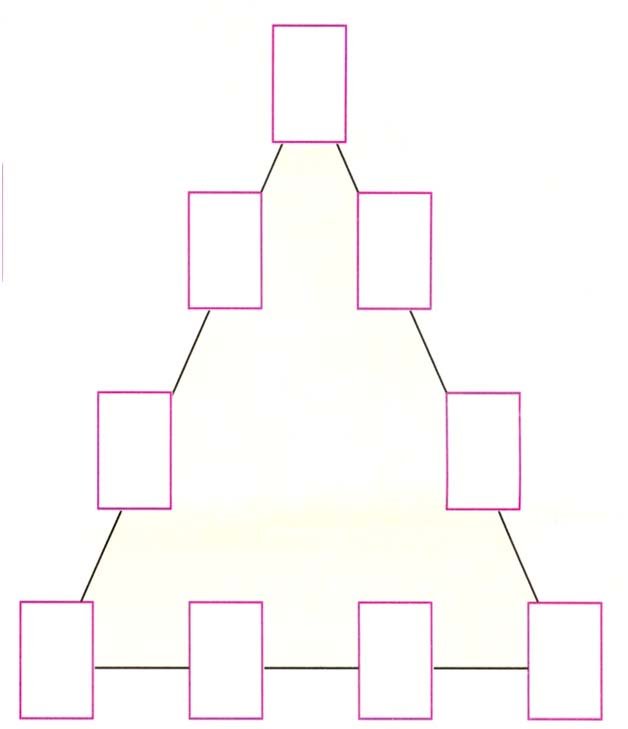
Q.No.18
There are ten sunflower plants. Plant them in five rows, each row containing four plants. The rows can be in any direction. The trees of one row can be counted in the other row if they make a straight row.

Q.No.19
Fill the numbers from 0 to 9 in the circles in such a way that no two consecutive numbers are connected by a straight line.

Q.No.20
Fill the circles with numbers from 1 to 9 such that each three circles shown by arrow add up to 13. Each number should be used only once.

Q.No.21
Put the numbers in the missing square so that each row, column and diagonal adds up to the same total.

Q.No.22
Fill the numbers from 1 to 9 only once, so that numbers, outside the circles represent the sum of the numbers in the four surrounding circles.
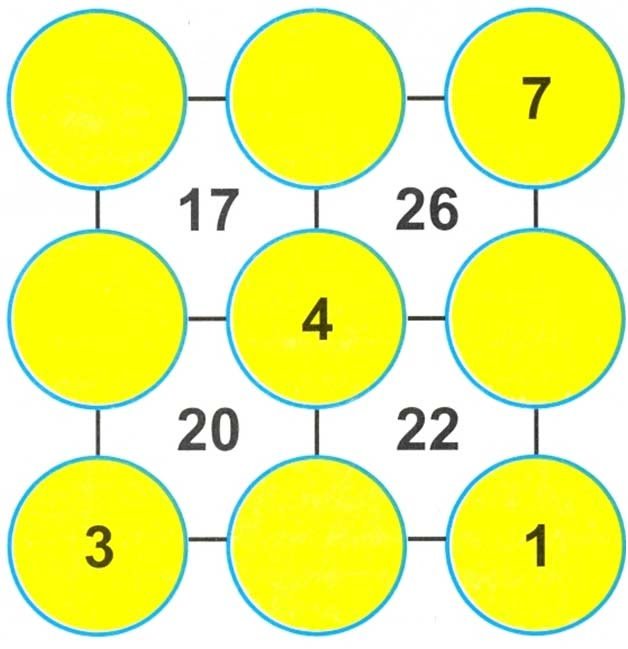
Q.No.23
The number written in triangles on the left for the across sum and on the top for the down sums. Fill the numbers only from 1 to 9 without repeating any number.

Q.No.24
Find a continue route on the numbers in such a way that while adding all the numbers on the way add to be exactly 100 at the ‘finish number’ start from the ‘start number’.

Q.No.25
Fill the numbers from 1 to 4 in such a way that each column, row and stream must contain different numbers.
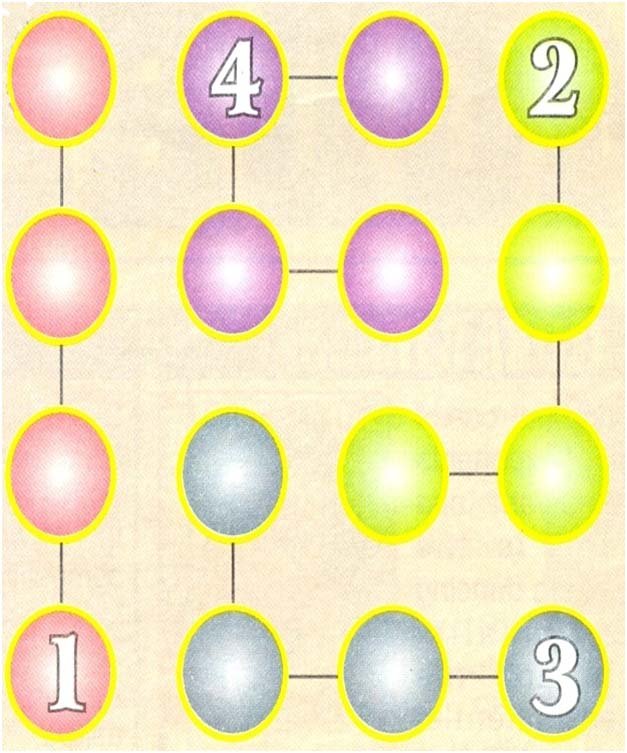
Q.No.26
Fill the numbers from 1 to 9 without repeating any number.
(a) The sum of the numbers of the five circles on all the four sides forming an angular shape equals to the number inside the angle which is outside the circle.
(b) Count the central circle as a vertex circle common in all the four angular circles.

Q.No.27
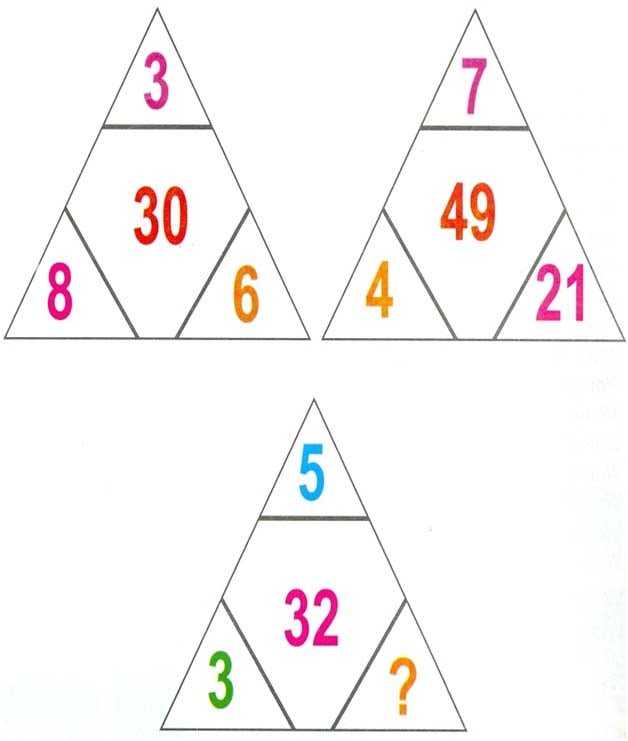
Make a pattern from the below two triangles and replace the question mark (?) in the bottom third triangle.
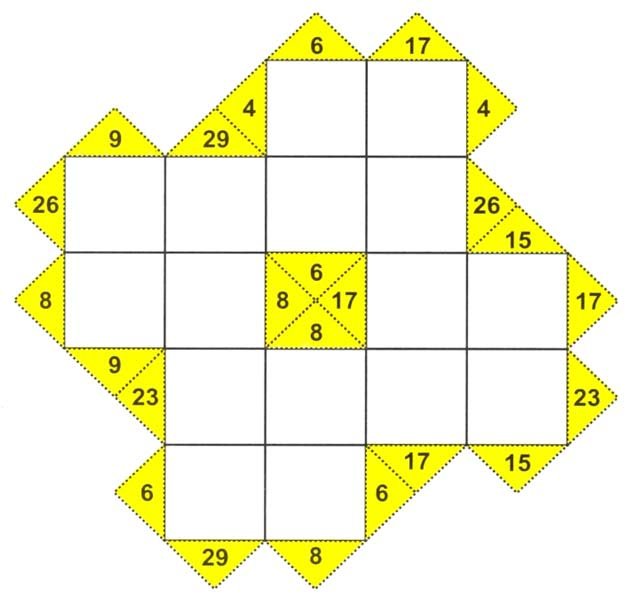
Q.No.28
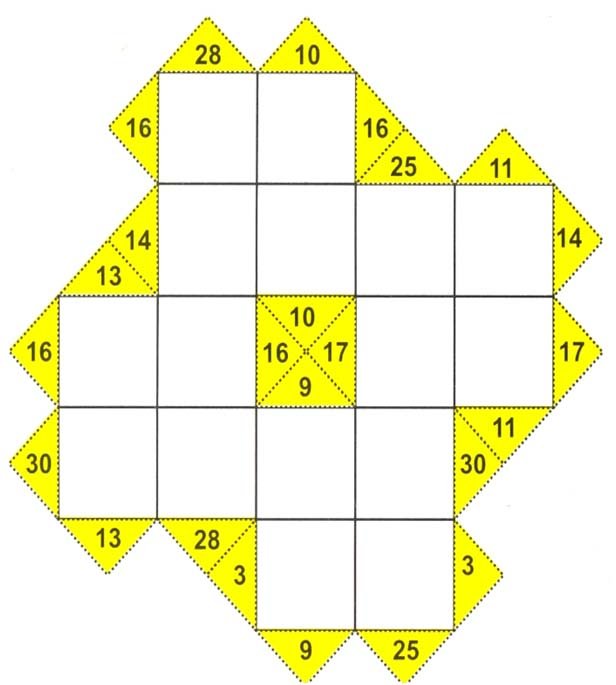
KAKURO PUZZLES
The numbers written in the triangles are the clues to solve the puzzle.
(a) Place one digit from 1 to 9 in each white box.
(b) These digits must be placed in such a way that the sum of digits in each set of the consecutive white boxes (across or down) is the number given in the triangle.
Q.No.29
(a) Fill one digit from 1 to 9 in each white box.
(b) The results in triangles are written on the left for the across sum and on the top for the down sums.
Q.No.30
How to Find Square of any n 5 number
1. Where n is any positive integer starting from 1 to n.
2. Remember place the number 5 at unit digit.
Method
1. Add 1 to n, you will get n + 1.
2. Multiply n and n + 1. You will get n (n + 1)
3. Here Square of 5 is 25.
4. Place the number as shown below n (n + 1) 25 which will be the square of any n 5 number.
Let us take a few examples and putting the values in the formula we get ……
- To find (105)²
Here n = 10
n+1 = 11
n (n+1) = 10 x 11 = 110
5² = 25
= TTh Th H T O
.·. (105)² = 1 1 0 2 5 - To find (65)²
Here n = 6
n+1 = 7
n(n+1) = 42
(5)² = 25
= Th H T O
.·. (65)² = 4 2 2 5 - To find (95)²
Here n = 9
n + 1 = 9 + 1 = 10
n (n+1)= 9 × 10 = 90
5² = 25
(95)² = 9025 - To find (625)²
Here n = 62
n + 1 = 63
n (n+1) = 62 x 63 = 3906
5² = 25
(625)² = 390625

